数学系の処理を扱うMathfの全変数と全関数【Unity】

この記事でのバージョン
Unity 5.3.1f1 Personal

目次

はじめに

表題通り、数学関係の関数や変数を持ったクラス、

Mathfの全変数、全関数を使用例なんかも交えながらご紹介！

Static 変数

変数とありますが、読み取りのみで、変動もしないので定数ですね。

一応、リファレンスには変数とあったので変数です！

度とラジアンの変換(Deg2Rad, Rad2Deg)

度からラジアンに変換するためにはDeg2Radを

ラジアンから度に変換するためにはRad2Degを使います。

float deg = 30.0f;//度
float rad = deg * Mathf.Deg2Rad;//ラジアン

float rad = 10.0f;//ラジアン
float deg = rad * Mathf.Rad2Deg;//度

以下の記事のように三角関数を使う時によくお世話になるやつ。

あとUnityとは関係ないですけど、Googleでも度からラジアンの変換できるんですね。

極小(Epsilon)

ごくわずかな浮動小数点の値を表す時はEpsilonを使います。

Debug.Log ("Mathf.Epsilon = " + Mathf.Epsilon);

Mathf.Epsilon = 1.401298E-45

1.401298E-45とは

0.000000000000000000000000000000000000000000001401298464324817

のことです。ちっちゃい！

無限大(Infinity, NegativeInfinity)

無限大を表す時はInfinityを

負の無限大を表す時はNegativeInfinityを使います。

Debug.Log (Mathf.Infinity);
Debug.Log (Mathf.NegativeInfinity);

Infinity
−Infinity

InfinityやNegativeInfinity自体はfloatですが、上記の通りLogで見ても特に数値は出ないんですね。

円周率(PI)

円周率を表す時はPIを使います。

Debug.Log (Mathf.PI);

3.141593

およそ3！

Static 関数

続いて関数です！

絶対値(Abs)

絶対値を得たい時はAbsを使います。

Debug.Log(Mathf.Abs(0.5f));
Debug.Log(Mathf.Abs(-120));

0.5
120

int OR floatが使えます。

floatの比較(Approximately)

floatの比較を行いたい時はApproximatelyを使います。

よくある浮動小数点の誤差による真偽の判定ミスを無くすための関数

例えば、以下のような感じ。

float value = 0;
for (int i = 0; i < 100; i++){
  value += 0.01f;
}

Debug.Log (value);
Debug.Log ((value == 1f));
Debug.Log (Mathf.Approximately(value, 1f));

0.9999993
False
True

0.01を100回足して、1にしたつもりが、丸め誤差が発生し==ではFalseが出てしまっています。

しかしこんな場合でもApproximatelyならTrueの判定が出せるってわけです。

切り上げ、切り捨て、四捨五入(Ceil, CeilToInt, Floor, FloorToInt, Round, RoundToInt)

小数点の

切り上げを行いたい時はCeilを

切り捨てを行いたい時はFloorを使います。

四捨五入を行いたい時はRoundを使います。

Debug.Log (Mathf.Ceil(1.4f));//切り上げ
Debug.Log (Mathf.Floor(1.4f));//切り捨て
Debug.Log (Mathf.Round(1.4f));//四捨五入

Debug.Log (Mathf.Ceil(3.7f));//切り上げ
Debug.Log (Mathf.Floor(3.7f));//切り捨て
Debug.Log (Mathf.Round(3.7f));//四捨五入

2
1
1

4
3
4

さらにToIntを付けたものは返り値がIntになるのでキャストする必要がなくなります。

最小、最大(Min, Max)

いくつかの値のうち、

最小の値を取得したい時はMinを

最小の値を取得したい時はMaxを使います。

Debug.Log (Mathf.Min(0.1f, 0.5f));
Debug.Log (Mathf.Max(585, 431));

//3つ以上の候補でもok
Debug.Log (Mathf.Max(1000, 431, 2301, 585, 1510));

//Listを使う場合はToArrayでfloat[]に変換して使う
List<float> list = new List<float> () {
  0.3f, -1.5f, 0.001f, 0f, -5.5f, 4.6f
};

Debug.Log (Mathf.Min(list.ToArray()));

0.1
585

2301

−5.5

int OR floatが使えます。

また、上記の例の通り、3つ以上の候補の中から選択する事もできます。今知りました！

範囲内に制限(Clamp, Clamp01)

値を一定の範囲内に制限したい時はClampを使います。

またClamp01を使うとminが0、max1の範囲内で制限します。

float value = 10, min = -5, max = 5;
Debug.Log (Mathf.Clamp(value, min, max));//valueを-5 ~ 5 の間に制限
Debug.Log (Mathf.Clamp01(value));//valueを0 ~ 1 の間に制限

5
1

なお、値が範囲内かどうか判定するメソッドはMathfにはないので、自前で作ってみました。

対数(Log, Log10)

対数を得たい時はLogを

常用対数(底が10の対数)を得たい時はLog10を使います。

int logarithm = 8, baseNum = 2;
Debug.Log (Mathf.Log(logarithm, baseNum));//log2 8
Debug.Log (Mathf.Log10(100));//log10 100

3
2

乗数(Pow, Exp)

乗数を得たい時はPowを

ネイピア数e(自然対数の底)の乗数を得たい時はExpを使います。

float value = 12, power = 3;
Debug.Log (Mathf.Pow(value, power));//12^3
Debug.Log (Mathf.Exp(power));//e^3

1728
20.08554

2のべき乗関係(ClosestPowerOfTwo, NextPowerOfTwo, IsPowerOfTwo)

ある値にもっとも近い2のべき乗を得たい時はClosestPowerOfTwoを

ある値以上でもっとも近い2のべき乗を得たい時はNextPowerOfTwoを

2のべき乗か判定したい時はIsPowerOfTwoを使います。

Debug.Log(Mathf.ClosestPowerOfTwo(7));//7にもっとも近い2のべき乗
Debug.Log(Mathf.ClosestPowerOfTwo(139));//139にもっとも近い2のべき乗

Debug.Log(Mathf.NextPowerOfTwo(7));//7以上でもっとも近い2のべき乗
Debug.Log(Mathf.NextPowerOfTwo(139));//139以上でもっとも近い2のべき乗

Debug.Log(Mathf.IsPowerOfTwo(139));//139が2のべき乗かどうか
Debug.Log(Mathf.IsPowerOfTwo(256)); //256が2のべき乗かどうか

8
128

8
256

False
True

平方根(Sqrt)

平方根を得たい時はSqrtを使います。

Debug.Log(Mathf.Sqrt(16));

4

符号(Sign)

符号を得たい時はSignを使います。

Debug.Log(Mathf.Sign(15214));
Debug.Log(Mathf.Sign(-3.5f));

1
−1

三角関数(sin, cos, tan)

三角関数はsin, cos, tanを使います。

float angle = 30f * Mathf.Deg2Rad;

Debug.Log(Mathf.Sin(angle));//サイン
Debug.Log(Mathf.Cos(angle));//コサイン
Debug.Log(Mathf.Tan(angle));//タンジェント

0.5
0.8660254
0.5773503

逆三角関数(Asin, Acos, Atan)

逆三角関数はAsin, Acos, Atanを使います。

float angle = 30f * Mathf.Deg2Rad;

Debug.Log(Mathf.Asin(angle));//アークサイン
Debug.Log(Mathf.Acos(angle));//アークコサイン
Debug.Log(Mathf.Atan(angle));//アークタンジェント

0.5510696
1.019727
0.4823479

角度(Atan2)

2点間の角度を得たい時はAtan2を使います。

// p2からp1への角度を求める
// @param p1 自分の座標
// @param p2 相手の座標
// @return 2点の角度(Degree)
public float GetAim(Vector2 p1, Vector2 p2) {
  float dx = p2.x - p1.x;
  float dy = p2.y - p1.y;
  float rad = Mathf.Atan2(dy, dx);
  return rad * Mathf.Rad2Deg;
}

角度差(DeltaAngle)

角度差を得たい時はDeltaAngleを使います。

返り値は-180~180の間になります。

Debug.Log (Mathf.DeltaAngle(50, 1200));

70

補完(Lerp, LerpUnclamped, LerpAngle, SmoothStep)

最小値min、最大値maxとした時に、

任意の比率の値を取得したい時はLerpを使います。

なお、比率は0~1の間で、それを超えた場合はminとmaxの値に制限されます。

比率が0~1を超えても制限されたくない時はLerpUnclampedを使います。

float min = 1.0f, max = 3.0f;

Debug.Log (Mathf.Lerp(min, max, 0.8f));
Debug.Log (Mathf.Lerp(min, max, -123));
Debug.Log (Mathf.Lerp(min, max, 5.7f));

Debug.Log (Mathf.LerpUnclamped(min, max, 0.8f));
Debug.Log (Mathf.LerpUnclamped(min, max, -123));
Debug.Log (Mathf.LerpUnclamped(min, max, 5.7f));

2.6
1
3

2.6
−245
12.4

Lerpを角度で使いたい時はLerpAngleを使います。

機能はLerpと同じですが、返り値が-180~180の間になります。

Debug.Log (Mathf.Lerp(0, 1000, 0.5f));
Debug.Log (Mathf.LerpAngle(0, 1000, 0.5f)); 

500
−40

SmoothStepも機能的にはLerpと一緒ですが、値の変化の仕方が違います。

Lerp(Linear interpolation)は比率を増やせば、min~maxの間を単純に増加していきます。

グラフにすると以下のような感じ。

それに対してSmoothStepは、最初と最後の増加量が少なくなります。

グラフにすると以下のような感じ。

逆補完？正規化?(InverseLerp)

aを0、bを1とした時、valueが0~1のいくらになるかを取得したい時はInverseLerpを使います。

ただし、返り値が0~1を超えた場合は0または1に制限されます。

//5を0、12を1とした時、8がいくつ(0~1)になるか
float a = 5f, b = 12f, value = 8;
Debug.Log (Mathf.InverseLerp(a, b, value));

0.4285714

日本語の説明だけだと分かり辛いと思ったので、

InverseLerpを使わないで同様の機能を実装してみました。

float a = 5f, b = 12f, value = 8;
float answer = 0; 

if(a!= b){
  answer = (value - a) / (b - a);//ここが重要
} 

answer = answer > 1 ? 1 : answer;
answer = answer < 0 ? 0 : answer;

Debug.Log (answer); 

0.4285714

こっちの方が分かり易いはず？

変化量を指定して増減 (MoveTowards, MoveTowardsAngle)

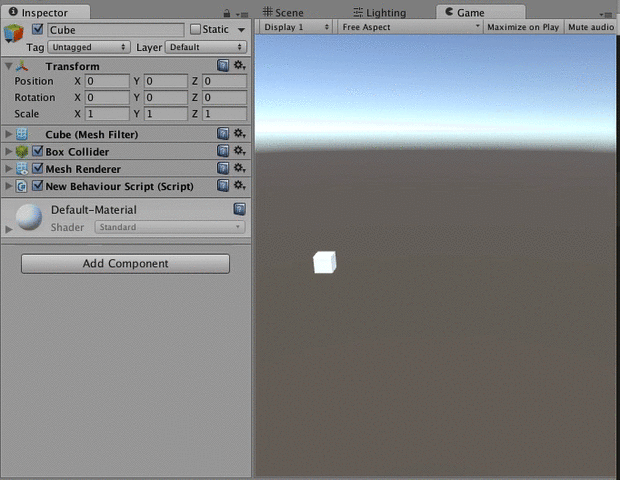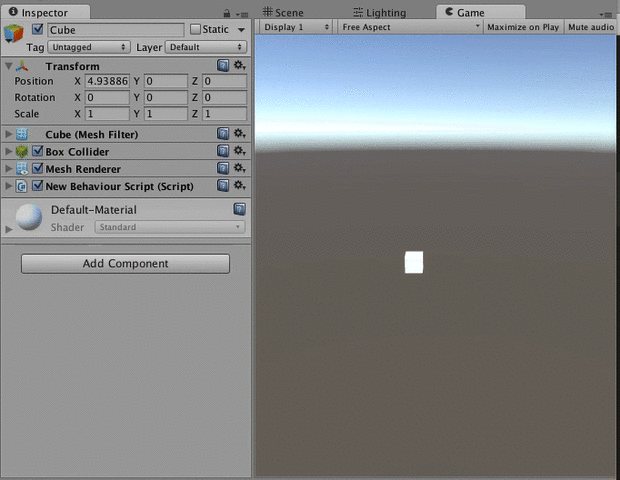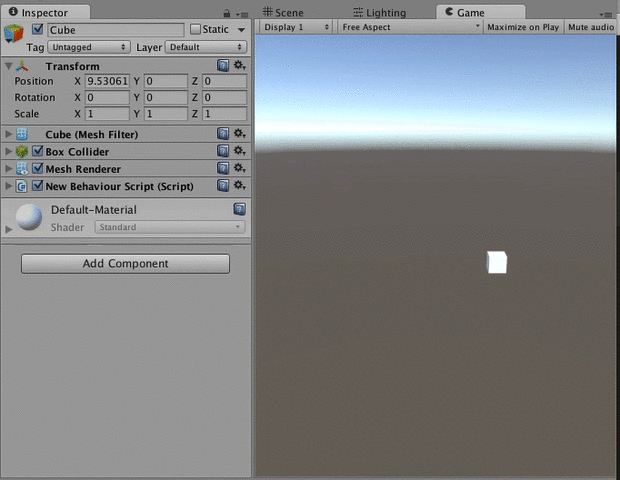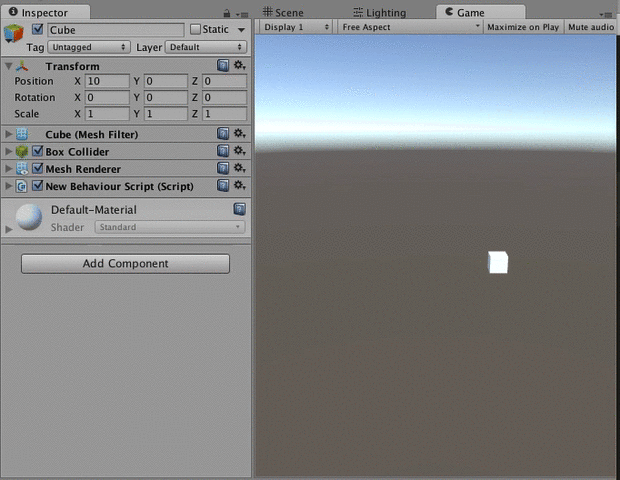
変化量を指定して増減させたい時はMoveTowardsを使います。

地点aから地点bまで速度vで移動したい、みたいな時です。

実際に使って見ると下のような感じです。

private void Update () {
  Vector3 position = transform.position;

  //position.xから10まで、1秒で10の速度で進む
  position.x =  Mathf.MoveTowards (position.x, 10, 10 * Time.deltaTime);

  transform.position = position;
}

なお、同様の処理を角度に行いたい時はMoveTowardsAngleを使います。

変化時間を指定して増減 (SmoothDamp, SmoothDampAngle)

変化時間を指定して増減させたい時はSmoothDampを使います。

地点aから地点bまで時間tで移動したい、みたいな時です。

実際に使ってみると以下のような感じです。

private void Update () {
  Vector3 position = transform.position;

  //position.xから10まで、0.1秒で進む。ただし最大速度はmaxSpeed。
  //現在の速度はcurrentVelocity、前回呼び出された時からの経過時間はTime.deltaTime
  //maxSpeedとtime.deletatimeは無くてもok
  float currentVelocity = 0, smoothTime = 0.1f, maxSpeed = 100;
  position.x =  Mathf.SmoothDamp (position.x, 10, ref currentVelocity, smoothTime, maxSpeed, Time.deltaTime);

  transform.position = position;
}

上記の例では毎フレーム開始位置が違うため、

0.1から10まで0.1秒で移動出来る速さで移動する、

0.2から10まで0.1秒で移動出来る速さで移動する、

0.3から10まで0.1秒で移動出来る速さで移動する、

みたいな感じで、減速していっています。

なお、同様の処理を角度に行いたい時はSmoothDampAngleを使います。

繰り返し動作(Repeat, PingPong)

繰り返し動作をする時はRepeatを使います。

と、言ってもRepeat自体がなにかを繰り返すわけではなく、

%を使って余りを計算するのと似た操作を行います。

実際に使ってみると以下のような感じです。

private void Update() {
  //Time.timeは経過時間、xは0→1、0→1、…、の動作をする
  transform.position = new Vector3(Mathf.Repeat(Time.time, 1), transform.position.y, transform.position.z);

  //以下も同様の動作をする
  //transform.position = new Vector3(Time.time % 1, transform.position.y, transform.position.z);
}

%を使って余りを求めた場合との違いは、返り値に負の値が帰ってこない事です。

Debug.Log ((0.5f % 0.3f));
Debug.Log (Mathf.Repeat(0.5f, 0.3f));

Debug.Log ((-5f % 0.3f));
Debug.Log (Mathf.Repeat(-5f, 0.3f));

0.2
0.2

−0.1999998
0.1000002

また、切り返すように繰り返し動作をする時はPingPongを使います。

実際に使ってみると以下のような感じです。

private void Update() {
  //Time.timeは経過時間、xは0→1、1→0、…、の動作をする
  transform.position = new Vector3(Mathf.PingPong(Time.time, 1), transform.position.y, transform.position.z);
}

パーリンノイズ(PerlinNoise)

パーリンノイズを利用したい時はPerlinNoiseを使います。

Debug.Log(Mathf.PerlinNoise (0.5f, 0.5f));

0.2966959

パーリンノイズの用途については以下の記事を参照の事。

カラー空間の変換(GammaToLinearSpace, LinearToGammaSpace)

ガンマスペースからリニアスペースへ値を変換したい時はGammaToLinearSpaceを使います

リニアスペースからガンマスペースへ値を変換したい時はLinearToGammaSpaceを使います。

そもそもリニアとかガンマとかなんぞやって話ですが、

ガンマとは、入力情報と出力情報のバランスのことです。

ガンマ1.0の環境をリニアスペースと呼び、入力された情報はそのまま出力されます。確かに理想的ですが、ありえません。

入力情報をそのままディスプレイに出力すると暗いため、補正するのが普通で、

その補正値をガンマと呼び、

ガンマが1.0、つまり補正されいない状態をリニアと呼ぶという事ですね。

実際に使ってみると以下のような感じです。

Debug.Log (Mathf.LinearToGammaSpace (0.5f)); 

0.7353569

使い所は分かりません( ´・◡・｀)ｵｼｴﾃ

おわりに

そもそもC#にはMathという、数学クラス(?)が用意されていますが、

Mathはdoubleが使われているので、基本的にfloatを使うUnityには使い辛かったりします。

System.Math uses doubles, UnityEngine.Mathf uses floats. Since Unity uses floats, it's generally better to use Mathf so you're not constantly converting floats/doubles.

http://forum.unity3d.com/threads/unityengine-mathf-vs-system-math.142539/

とりあえず、特に理由が無ければMathfの方を使えば良さそうです。

---